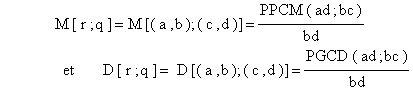Remarque :

Pour a Î N^* et b Î N^* on a : a |_Q b Û b Î aN^* Û a | b

La relation |_Q sera donc dorénavant notée simplement : |

Définition - 3 :

Pour des entiers a, b, c et d on pose :

Propriétés - 1 :

Pour des entiers a, b, c, d, a’, b’, c’ et d’ :

(p₁) : M[(c,d) ;(a,b)] = M[(a,b) ;(c,d)] et D[(c,d) ;(a,b)] = D[(a,b) ;(c,d)]

(p₂) : si ab’ = ba’ alors M[(a’,b’) ;(c,d)] = M[(a,b) ;(c,d)]

et D[(a’,b’) ;(c,d)] = D[(a,b) ;(c,d)]

(p₃) : si ab’ = ba’ et cd’ = dc’ alors M[(a’,b’) ;(c’,d’)] = M[(a,b) ;(c,d)]

et D[(a’,b’) ;(c’d’)] = D[(a,b) ;(c,d)]

Démonstrations - 1 :

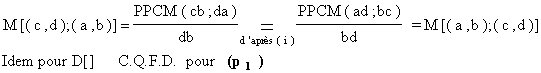
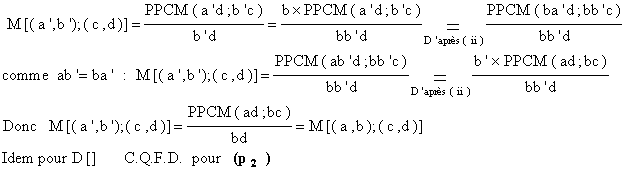
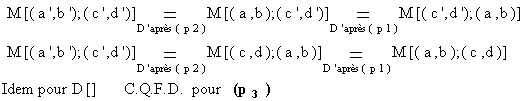
Définition - 4 :

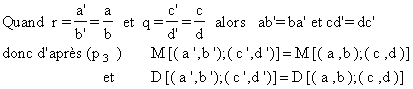
Les définitions de M[] et D[] ne dépendent donc pas du choix des représentants

fractionnaires des rationnels r et q . On peut alors définir :