PGCD et PPCM dans Q

Préambule :

Les notions de multiple, diviseur, PGCD et PPCM sont définies (et supposées connues) dans N^*.

Nous nous proposons de les étendre à l’ensemble Q^+*.

Notations :

- N^* est l’ensemble des entiers naturels non nuls et

Q^+* celui des rationnels strictement positifs .

Désormais quand on parlera d’entiers il s’agira d’éléments de N^*

de même un rationnel sera supposé appartenir à Q^+*.

- aN^* est l’ensemble des multiples de a dans N^*.

- On note | la relation « ... divise ... »

- PPCM(a;b) et PGCD(a;b) sont respectivement le Plus Petit Commun Multiple et

le Plus Grand Commun Diviseur des entiers a et b.

Propriétés admises et définition utilisée :

(i) PPCM(b;a) = PPCM(a;b) et PGCD(b;a) = PGCD(a;b)

(ii) PPCM(na;nb) = n PPCM(a;b) et PGCD(na;nb) = n PGCD(a;b)

(iii) PPCM(a;b) ´ PGCD(a;b) = a ´ b

(iv) a | b Þ PPCM (a;b) = b et PGCD(a;b) = a

(v) Si a £ b alors PGCD(a;b) £ a £ b £ PPCM (a;b)

(vi) a | PPCM (a;b) , b | PPCM (a;b) et PGCD(a;b) | a , PGCD(a;b) | b

(vii) Deux entiers a et b sont dits étrangers si PGCD(a;b) = 1

D’après (iii) : a et b sont dits étrangers Û PPCM(a ;b) = a ´ b

Définition - 1 :

Pour tout rationnel r on appelle Q-multiples de r les nombres q de la forme

m ´ r où m est un entier.

Remarque :

Pour un entier a : p est un Q-multiple de a Û p est un multiple de a

Les notions de multiple et de Q-multiple se confondent donc pour les

nombres entiers. Alors on notera rN^* l’ensemble des Q-multiples de r.

Exemples :

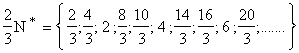
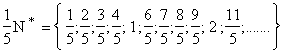
Remarque :

Définition - 2 :

Pour deux rationnels r et q on dira que r Q-divise q (notation : r |_Q q)

si q est un Q-multiple de r.

c.àd. . r |_Q q Û q Î rN^* Û $ un entier m tq : q = m ´ r